ECM Performance Model
Introduction
The ECM (Execution-Cache-Memory) performance model is a resource-based analytic performance model. It can predict the runtime of serial straight-line code (usually an inner-most loop body) on a specific processor chip. Runtime predictions are based on a maximum throughput assumptions for instruction execution as well as data transfers, but refinements can be added. The model in its simplest form can be set up with pen and paper.
Description
The model decomposes the overall runtime into several contributions, which are then put together according to a machine model. A processor cycle is the only time unit used. All runtime contributions are provided for a number of instructions required to process a certain number of (source) loop iterations; we typically choose one cache line length (e.g., 8 iterations for a double precision code), which makes sense because the smallest unit of data that can be transferred between memory hierarchy levels is a cache line. For simple calculations bandwidths and performance are consistently specified in “cycles per cache line.” However, this choice is essentially arbitrary, and one could just as well use “cycles per iteration.” Unless otherwise specified, an “iteration” is one iteration in the high-level code.
In-core model
The primary resource provided by a CPU core is instruction execution. Since instructions can only be executed when their operands are available, the in-core part of the ECM model assumes that all data resides in the innermost cache. It further assumes out-of-order scheduling and speculative execution to work perfectly so that all the instruction-level parallelism available in the code can be provided by the hardware, resources permitting (on a given microarchitecture).
In practice, the first step is to ignore all influences preventing maximum instruction throughput, such as:
- Out-of-order limitations
- Instruction fetch issues
- Instruction decoding issues
- Complex register dependency chains
Loop-carried dependencies and long latency instructions should be considered, though. The in-core model thus delivers an optimistic execution time for the code (in cycles per iteration) in which all data transfers beyond the innermost cache are ignored.
Data transfer model
Data transfers are a secondary resource required by code execution. Modeling data transfers starts with an analysis of the data volume transferred over the various data paths in the memory hierarchy. Some knowledge about the CPU architecture is required for this in order to know what path cache lines take to get from their initial location into L1 cache and back. It is assumed that latencies can be perfectly hidden by prefetching, so all transfers are bandwidth limited. Additional data transfers from cache conflicts are neglected (it is still possible to extend the model to account for additional transfers). Together with known (or measured) maximum bandwidths, the data transfer analysis results in additional runtime contributions from every data path. How to put together these contributions with each other and with the in-core execution time is part of the machine model. The two extreme cases are:
- Full overlap: The predicted execution time is the maximum of all contributions.
- No overlap: The predicted execution time is the sum of all contributions
There is s large gray zone in between these extremes. On most modern Intel Xeon CPUs, data transfer times must be added up and everything that pertains to “work” (i.e., arithmetic, loop mechanics, etc.) overlaps with data transfers. This yields the most accurate predictions on these CPUs, but other architectures behave differently.
Example: Double precision “Schönauer” vector triad (Figure 1)
for (int i=0; i<size; i++) {
A[i] = B[i] + C[i] * D[i];
}
Machine specs
For this example we assume a hypothetical processor running at 2.7 GHz with the following specs:
- It can execute one 32-byte SIMD vectorized add and one 32-byte SIMD vectorized multiply instruction per cycle.
- Superscalar , out-of-order execution with a maximum instruction throughput of four per cycle.
- One 32-byte wide load and one half 32-byte wide store instruction per cycle and core.
- The bandwidth between L1 and L2 cache is 32 bytes/cycle and the cache line size is 64 byte. This results in an L1-L2 bandwidth of 2 cycles per cache line transfer.
- The cache hierarchy is inclusive and uses a write-back policy for stores. Therefore every store miss causes an additional write-allocate transfer.
- The sustained (saturated, i.e., using all cores) memory bandwidth is 40 GB/s or 4.3 cycles per cache line transfer. This is the only measured quantity that enters the model.
Code specs
The vectorized code performs one (SIMD) multiply and one (SIMD) add instruction and requires 3 (SIMD) loads and 1 (SIMD) store. We assume we use the 32-byte SIMD instruction set. This results in 2 multiply, 2 add, 6 load, and 2 store instructions to process one cache line length of high-level iterations (8).
In-core and data transfer analysis
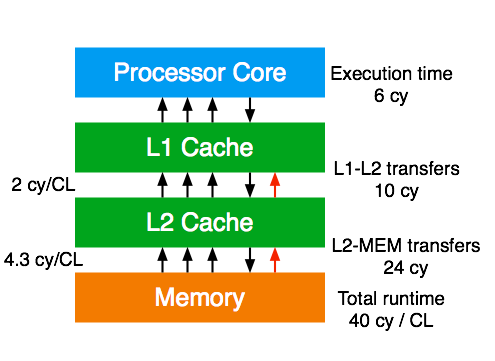
First we map the code on the machine specs. For the instruction execution one has to find the unit which takes the longest time to finish the work. The 2 multiply and 2 add instructions take 2 cycles as the processor can execute a multiply and add in the same cycle. The six 32-byte load instructions take six cycles and the two 32-byte stores take 4 cycles. As a result of the core execution analysis we conclude that the in-core execution bottleneck is the load instruction throughput on this specific processor type. The core execution time to process 8 scalar iterations (equivalent to two 32-byte SIMD iterations) is 6 cycles.
To get the runtime contribution for the L2-L1 transfers we first determine the number of transferred cache lines. For eight iterations (one cache line length) of work we need to load 3 cache lines and store 1 cache line. Because the architecture triggers a write-allocate transfer on a store miss we need to add one more cache line transfer from L2 to L1. This results in 5 cache line transfers. The L1-L2 bandwidth is 2 cycles per cache line transfer, resulting in 10 cycles runtime contribution. The same data volume applies for the L2-MEM transfers, but the bandwidth is 4.3 cycles per cache line resulting in 21.5 cycles runtime contribution.
ECM model
We assume that the CPU is close to an Intel Xeon. Summing up all data transfer contributions gives a total runtime of 37.5 cycles per eight iterations. The arithmetic part (multiplies and adds) only takes 2 cycles and overlaps with the data transfers, so we can neglect it. Hence, the prediction is 37.5 cycles. One can convert this to more common performance metrics: The flop rate is (16 flops / 37.5 cycles) x 2.7 GHz = 1.15 Gflop/s. The resulting memory bandwidth is (5 x 64 bytes / 37.5 cycles) x 2.7 GHz = 23.0 Gbyte/s. There is an important insight here: One core only achieves roughly 58% of the saturated memory bandwidth because of the non-overlapping data transfers across the memory hierarchy. Out of 37.5 cycles, the memory bus is only used for 21.5.
If the characteristics of a processor are too poorly understood to come up with a useful machine model, one can assume “best case” and “worst case” scenarios, which may translate to the “full overlap” and “no overlap” models described above. In many cases the predictions thus made will be too far apart to be useful, though. A machine model will always contain some heuristics to make it work in practice. Note that the goal here is always to have a model that has predictive power. Whether or not some “(non-)overlap” assumptions are actually implemented in the hardware is an entirely different matter. In other words, the model may be wrong (because it is based on false assumptions) but still useful in terms of predictive power.
Extension to multi-core chips
The extension to multi-core is straightforward. The one core performance is scaled linearly until a shared bottleneck in the processor design is hit. This may be a shared cache or memory interface. The ECM model can predict if a code is able to saturate the memory bandwidth and how many cores are required to do so. We have recently extended the model to describe deviations from this simple behavior with great accuracy [Hofm2018].
What happens if the model “fails”?
If the model fails to deliver an accurate prediction or description of behavior (e.g., with changing problem size), this does not mean that it is useless. Failed attempts at modeling performance are always an opportunity to learn more about the problem: Maybe there was an overly optimistic assumption in the model, some peculiarity in the hardware that was overlooked, some miscalculation of data traffic, etc. Whatever the reason, a failure of the model must be regarded as a challenge. It is not the end of the process but a part of it.
This is also why we do not believe that performance modeling can be fully automated. Tools can help, but the scientist draws the final conclusions.
Conclusion
The main advantage of the ECM model is that apart of providing a performance estimate it also generates knowledge about different runtime contributions originating from different parts of the hardware and their relation to each other. It is a very useful tool for understanding observed performance and decide on optimizations for a wide range of codes, from simple streaming kernels to various stencil codes, medical image processing kernels, and the Lattice Boltzmann method.
Current and future research focus
While the predictive power of the model is significantly improved using heuristics for overlap estimates it still occurs that the model underestimates performance. Introducing a better heuristic for overlap prediction is on-going research. Another focus is to come up with a similar analytic model for codes with data transfers that are (partially) latency bound.
Setting up the model can be tedious, especially with large loop bodies. We develop tools that help to get the required input to formulate the model more easily: Kerncraft and OSACA.
Selected publications about the theory and applications of the ECM model
- G. Hager, J. Eitzinger, J. Hornich, F. Cremonesi, C. A. Alappat, and G. Wellein: Applying the Execution-Cache-Memory Performance Model: Current State of Practice. Poster accepted for SC18, Dallas, TX. SC18-Poster-ECM_PRINT_M.pdf
- J. Hofmann, G. Hager, and D. Fey: On the accuracy and usefulness of analytic energy models for contemporary multicore processors. In: R. Yokota, M. Weiland, D. Keyes, and C. Trinitis (eds.): High Performance Computing: 33rd International Conference, ISC High Performance 2018, Frankfurt, Germany, June 24-28, 2018, Proceedings, Springer, Cham, LNCS 10876, ISBN 978-3-319-92040-5 (2018), 22-43. DOI: 10.1007/978-3-319-92040-5_2, Preprint: arXiv:1803.01618. Winner of the ISC 2018 Gauss Award.
- J. Hofmann and D. Fey: An ECM-based Energy-efficiency Optimization Approach for Bandwidth-limited Streaming Kernels on Recent Intel Xeon Processors. In: IEEE Press (Ed.): Proceedings of the 4th International Workshop on Energy Efficient Supercomputing (E2SC), Salt Lake City, UT, USA, November 14, 2016, pp. 31-38. DOI: 10.1109/E2SC.2016.010
- J. Hofmann, D. Fey, M. Riedmann, J. Eitzinger, G. Hager, and G. Wellein: Performance analysis of the Kahan-enhanced scalar product on current multi- and manycore processors. Concurrency & Computation: Practice & Experience 29(9), e3921 (2017). Available online, DOI: 10.1002/cpe.3921.
- H. Stengel, J. Treibig, G. Hager, and G. Wellein: Quantifying performance bottlenecks of stencil computations using the Execution-Cache-Memory model. Proc. ICS15, the 29th International Conference on Supercomputing, June 8-11, 2015, Newport Beach, CA. DOI: 10.1145/2751205.2751240. Recommended as a good starting point to learn about the ECM model.
- M. Wittmann, G. Hager, T. Zeiser, J. Treibig, and G. Wellein: Chip-level and multi-node analysis of energy-optimized lattice-Boltzmann CFD simulations. Concurrency and Computation: Practice and Experience 28(7), 2295-2315 (2015). DOI: 10.1002/cpe.3489.
- G. Hager, J. Treibig, J. Habich, and G. Wellein: Exploring performance and power properties of modern multicore chips via simple machine models. Concurrency and Computation: Practice and Experience 28(2), 189-210 (2016). First published online December 2013, DOI: 10.1002/cpe.3180.
- J. Treibig and G. Hager: Introducing a Performance Model for Bandwidth-Limited Loop Kernels. Proceedings of the Workshop “Memory issues on Multi- and Manycore Platforms” at PPAM 2009, the 8th International Conference on Parallel Processing and Applied Mathematics, Wroclaw, Poland, September 13-16, 2009. Lecture Notes in Computer Science, Volume 6067, 2010, pp 615-624. DOI: 10.1007/978-3-642-14390-8_64.
