Success Story: Simulation of unconventional superconductors

Background

Superconductors are exotic materials that carry electric current with zero resistance and have wide reaching applications in energy transport, storage, sensor technology, and quantum computing. What stops them from being used in everyday life is that they are only operational at very low temperatures or very high pressures. High-temperature superconductors are rare and, despite decades of research, still not fully understood. Very recently, evidence for a room-temperature superconductor has been found [4], with new theoretical and numerical questions arising. In this project, we include for the first time realistic long-range interactions between electrons and simulate the quantum ground state of a two-dimensional superconductor, seeing new exotic phases of matter. These results, reported in [1], can guide the search for novel materials with potentially ground-breaking technological applications.

Superconductors have recently found their way into the media with several claims of room temperature superconductivity [5,6,7], underscoring the great interest in this field of research as well as the potential impact on society. Using computational techniques, it was revealed that the material in Ref. [8] is in fact not superconducting, yet exhibits other exotic properties, highlighting the importance of simulations for understanding exotic materials.

Computation

Simulating a superconductor means to solve the following Bardeen-Cooper-Schrieffer equation for the superconducting order parameter, the so-called gap \Delta(k) with k the two-dimensional wavevector, derived in [1],

\Delta(k) = \int \limits_{\mathrm{BZ}} \Big(C_0 + U_0 Z_{\Lambda,\nu}(k-q)\Big) \frac{\Delta(q)}{2\sqrt{\xi^2(q)+|\Delta(q)|^2}}\,\mathrm d q.

Here \xi(k) = \cos(2\pi k_1) + \cos(2\pi k_2) is the dispersion relation and C_0 and U_0 are material constants.

The long-range interaction is encoded in the Epstein zeta function Z_{\Lambda,\nu}, a generalization of Riemann zeta to a higher dimensional lattice \Lambda and an electron interaction that falls off with \vert x\vert^{-\nu}. This novel result has been recently derived in [2,3]. Solving above nonlinear integral equation is a challenging task in two dimensions, in particular as the Epstein zeta function becomes singular at q=0. After suitably interpolating \Delta with periodic splines, we solve for the spline coefficients with a numerical effort that scales quadratically in the number of discretization points N.

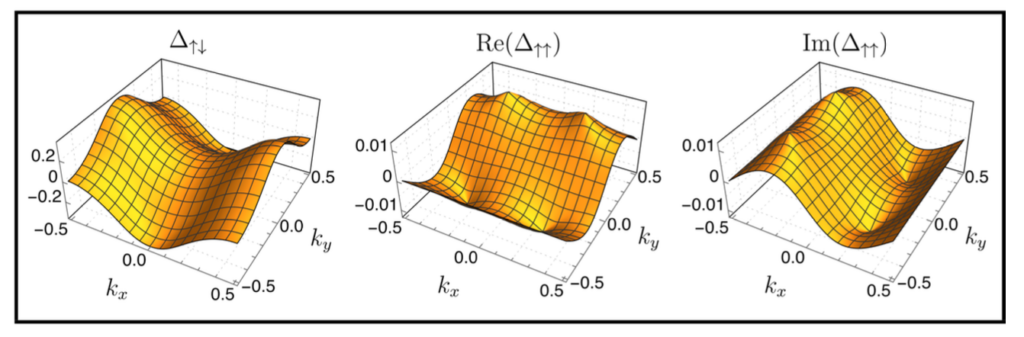
Above, an exotic solution to the gap equation is displayed [1].

We then move on to compute the phase-diagram as a function of two parameters \nu and U_0. This task is achieved in parallel, where any point in the diagram is computed on a separate node of the cluster, leading to the following result [1].

 

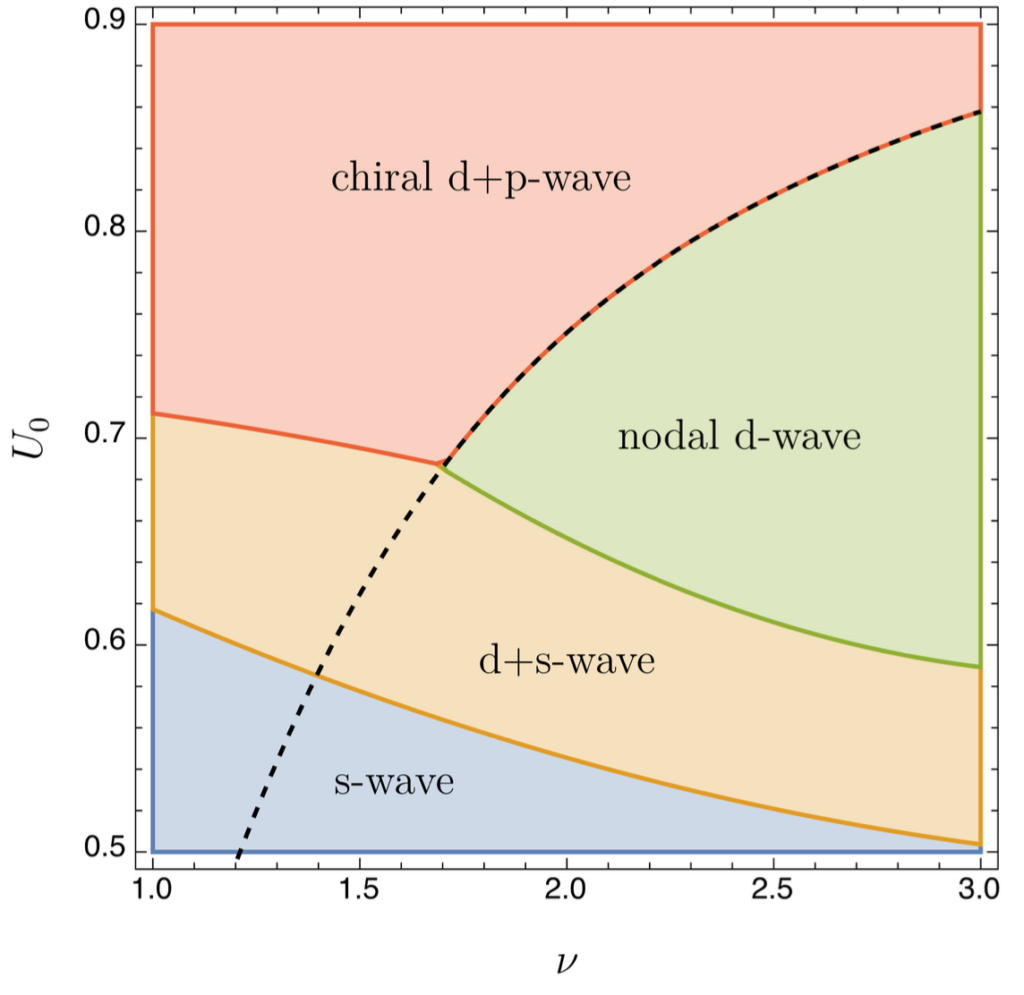
Here the different phases correspond to different symmetries in the arising gap function that completely change the physical properties of the material. The phases in red and yellow are new and solely arise due to the long-range interactions.

Analysis

During a test project at NHR@FAU, the NHR@FAU team approached the scientists to offer help in optimizing their code as monitoring data showed a low vectorization ratio.

The application makes heavy use of the data type complex_t and micro-benchmarks showed that some computation could be improved by separating the complex number into real and imaginary part explicitly and store them in separate arrays.

The code review inspired the scientist to look more closely at the quadratic effort in N that appears in all simulations of superconductors. Looking more closely at the integral operator, the scientist realized that an application of the Fast Fourier Transform (FFT) reduces the numerical effort as follows: N^2 \rightarrow N \log N
Unfortunately, a significant slowdown was noticeable by the OpenMP parallel computation of FFTs. The FFTW library uses OpenMP internally and thus caused nested parallelism with all second-level threads running on a single hardware thread.

Optimization

In order to improve vectorization and function inlining by the compiler, the relevant functions and declarations were moved to a single compilation unit. The vectorization was further improved by using vector intrinsics.

The idea to split the complex_t data type into its parts was not applied as the FFTW library relies on the data type and changing data types just for FFTW was not feasible.

By leveraging the feature of “plans” of the FFTW library, the execution behavior was improved as less setup is required for each FFT operation. Moreover, the second-level parallelism was deactivated.

Conclusion

After improving vectorization and transforming the problem into the frequency domain, the scientists achieve a speedup for a typical discretization of N=1024^2 of more than a hundredfold. The code optimizations reduced the originally estimated compute time requirements of approx. 50 Million core-hrs (10% of the annual NHR@FAU capacity) to less than 0.5 million core-hrs (typical capacity of a test project).

References

[1] Exact Continuum Representation of Long-range Interacting Systems and Emerging Exotic Phases in Unconventional Superconductors, Andreas A. Buchheit, Torsten Keßler, Peter K. Schuhmacher, and Benedikt Fauseweh, Phys. Rev. Research 5, 043065 (2023)
[2] Singular Euler-Maclaurin expansion on multidimensional lattices, Andreas A. Buchheit & Torsten Keßler, Nonlinearity 35 3706 (2022)
[3] On the Efficient Computation of Large Scale Singular Sums with Applications to Long-Range Forces in Crystal Lattices, Andreas A. Buchheit and Torsten Keßler, J. Sci. Comput. 90, 53 (2022)
[4] Dasenbrock-Gammon, N., Snider, E., McBride, R. et al. Evidence of near-ambient superconductivity in a N-doped lutetium hydride. Nature 615, 244–250 (2023)
[5] Lee, S. et al. Preprint at https://arxiv.org/abs/2307.12037 (2023).
[6] Lee, S., Kim, J.-H. & Kwon, Y.-W. Preprint at https://arxiv.org/abs/2307.12008 (2023)
[7] Guo, K., Li, Y. & Jia, S. Sci. China Phys. Mech. Astron. https://doi.org/10.1007/s11433-023-2201-9 (2023)
[8] Dan Garisto, LK-99 isn’t a superconductor — how science sleuths solved the mystery, Nature, ISSN 1476-4687, https://www.nature.com/articles/d41586-023-02585-7, 2023